ALTHOUGH I’M PROVIDING BOTH ONLINE AND OFFLINE TOOLS, ONLINE TOOLS SHOULD ONLY BE USED FOR EXPERIMENT PURPOSES, I WILL NOT BE HELD RESPONSIBLE FOR ANY ASSET LOSSES. IF YOU’RE SERIOUS ABOUT MNEMONIC SEED CREATION, DOWNLOAD ALL THE PROVIDED OFFLINE TOOLS, PUT THEM INSIDE A COMPLETELY AIR-GAPPED ENVIRONMENT (A COMPUTER WITHOUT ANY DRIVERS INSTALLED), AND USE THEM EXCLUSIVELY THERE. NEVER KEEP STUFF INSIDE THE CLIPBOARD AFTER DOING COPY-PASTE JOBS, AND DEFITELY DO NOT USE A MOBILE OPERATING SYSTEM.
Although there are many tools out there for creating a mnemonic seed for you, these tools are not risk free. That’s because you will have to trust the way these tools work and that the results are indeed random and not preloaded in the code of the program. For example, a malicious app may be programmed to give one out of ten thousand preloaded mnemonic seeds to the users, a number big enough to give the impression of true randomness, while the malicious programmer of the app is sitting and waiting for free money. Paranoid? Yes, but definitely not impossible to happen.
And although most of the seed generators are open source, the same thing cannot be said for software or hardware wallets. And even if you use an open source wallet generator, what’s better than doing the job manually.
WHAT EXACTLY IS A MNEMONIC SEED
A mnemonic seed is nothing more than a very large number transformed into words for the sake of convinience. HD wallets (thats not High Definition but stands for Hierarchical Deterministic) can use the mnemonic seed to create infinite addresses for every one of their supported coins.
TOOLS YOU’RE GOING TO NEED (DO NOT USE ONLINE TOOLS FOR ANYTHING ELSE THAN EXPERIMENTING)
PWGen (a powerful password generator, good enough for creating our entropy)
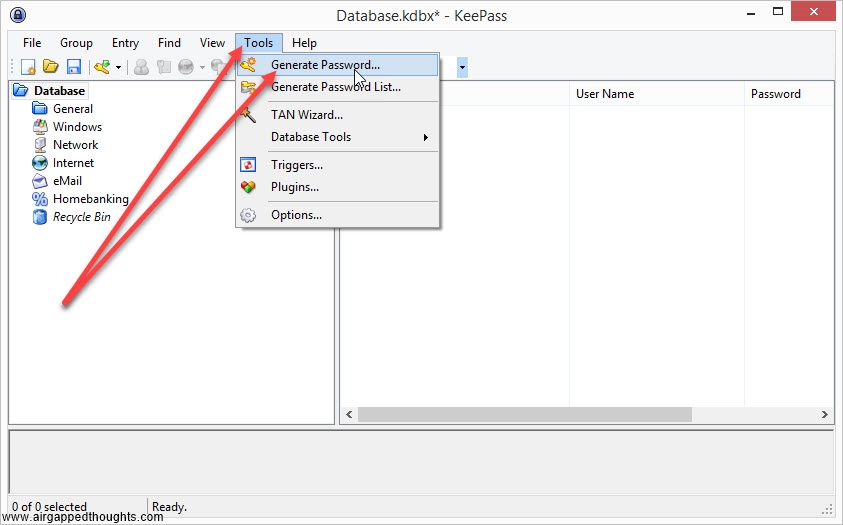
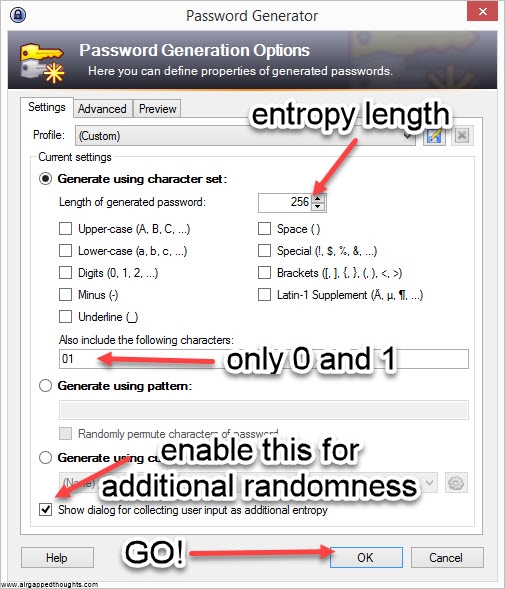
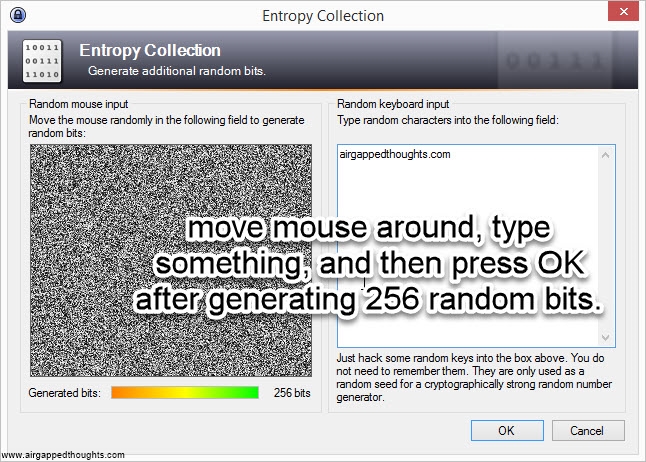
Keepass (an open source and cross platform password manager with an excellent password generator. Although the password generation is only one part of this app, its extremely powerful since it generates random entropy from user interaction. You can use this one over PWGen)
Hashing (a free hashing tool)
Hexprobe Multibyte Calculator (useful for every binary / decimal / hexadecimal conversion. can aslo do hashing and create random bits so technically this can replace every tool in this list but i do not recommend creating entropy with this tool).
LET’S DO THIS
1. The first and the most important step is the creation of our entropy. An entropy is a random value which is solely responsible for the end result. So it’s important to be as random as it can be. When you buy a hardware wallet and the company behind it is bragging about having embedded some king of true random number generator in it, it actually means that this entropy is generated using some unique methods that makes it impossible to be reproduced by other users.
We have a few options for creating entropy, you may have heard about the coin toss method: You take a coin, toss it multiple times, and keep track of the heads/tails results while tracking them down as 0 and 1. How many times do you have to toss the coin? That depends from the number of words you want to get for your mnemonic seed.
Every 11 tosses (eleven 0s and 1s) is 1 word but the last word will be added using a different method that involves cryptography so for starters you should just remember this:
128 tosses: 12 words seed
192 tosses: 18 words seed
256 tosses: 24 words seed
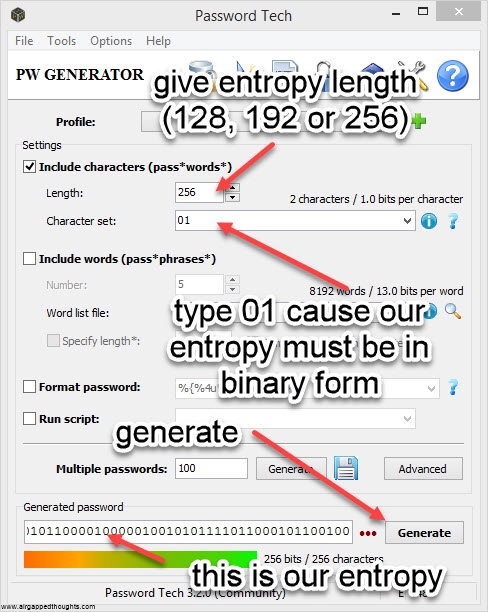
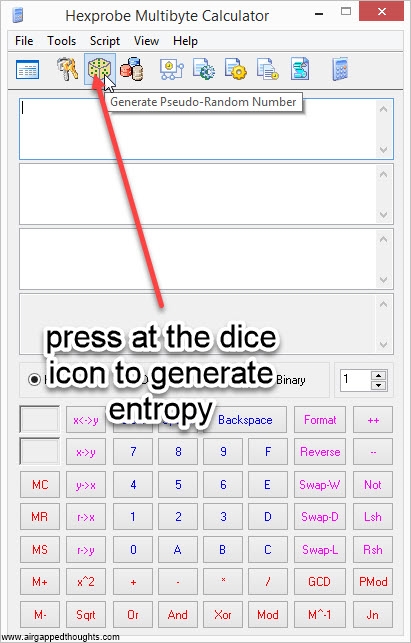
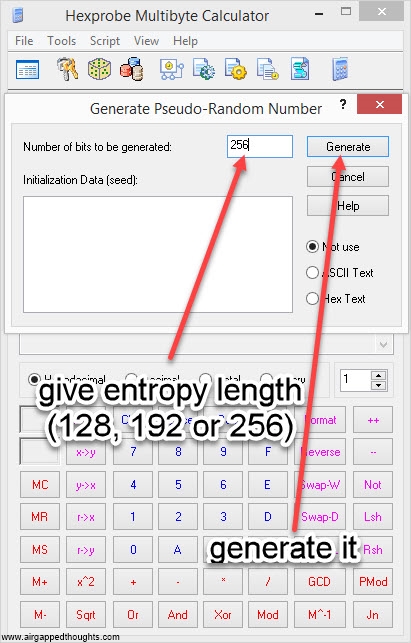
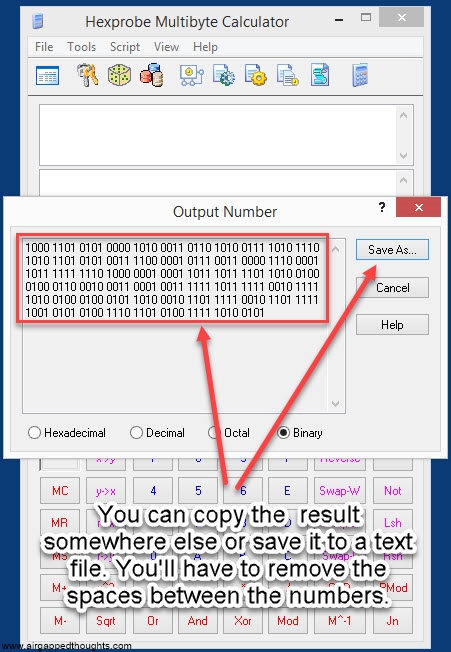
If you’re not in the mood for coin tossing, you can use PWGen or Keepass, or randomly type 128, 192 or 256 0s and 1s (not recommended). In our example we are going to create a 24 words mnemonic seed. I attach images with instructions for PWGen, Keepass (recommended) and Hexprobe Multibyte Calculator (not recommended):
PWGEN
KEEPASS
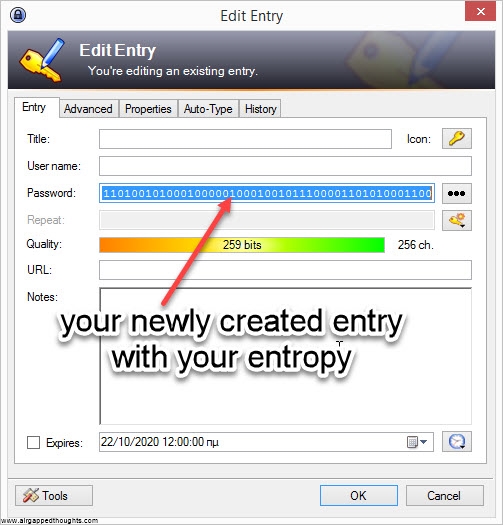
HEXPROBE MULTIBYTE CALCULATOR
So let’s take the following 256 bits as our entropy (generated through the PWGen app):
0111101001010000011110111000001000000101011101101001001001010010110101001101100001111111000011101010111111111010101100001101000011001101011100000101101110101001001011011111111101001101010010000011100001110111100111000101100010110110011110000000101001001011
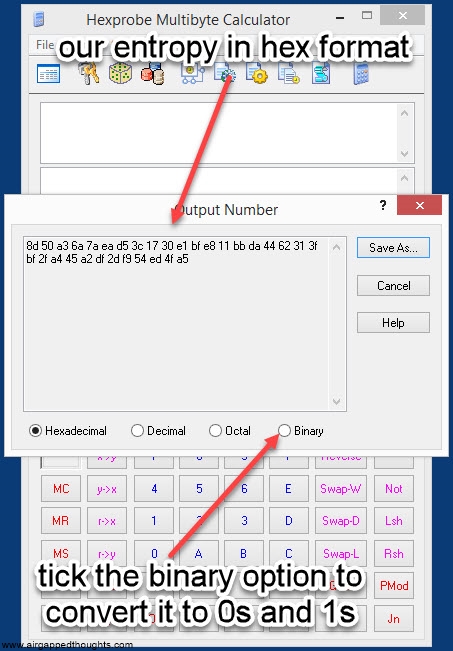
2. We now need to convert the above number in hexadecimal form. Use Hexprobe Multibyte Calculator for this. If you used this tool for generating entropy, you already have the hex value, if not, use the instructions below to import entropy from another app and convert it.
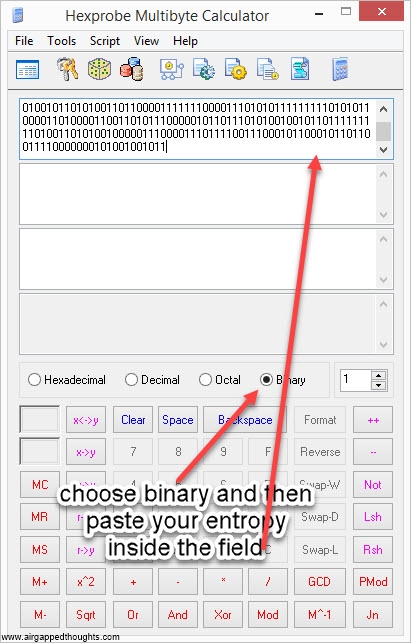
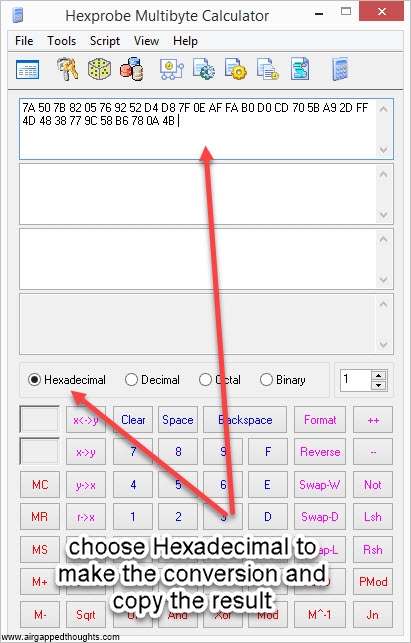
or go here and use the online tool (only for testing purposes, never use online tools).
Our entropy in hex format is:
7A507B8205769252D4D87F0EAFFAB0D0CD705BA92DFF4D4838779C58B6780A4B
Now he have to hash the above hexadecimal format into sha256. You can use the #ashing application
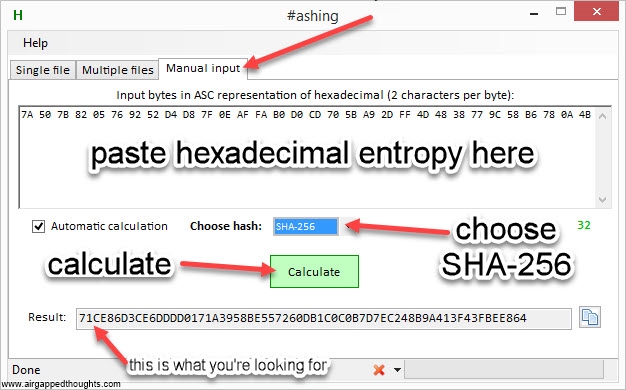
Or Hexprobe Multibyte Calculator
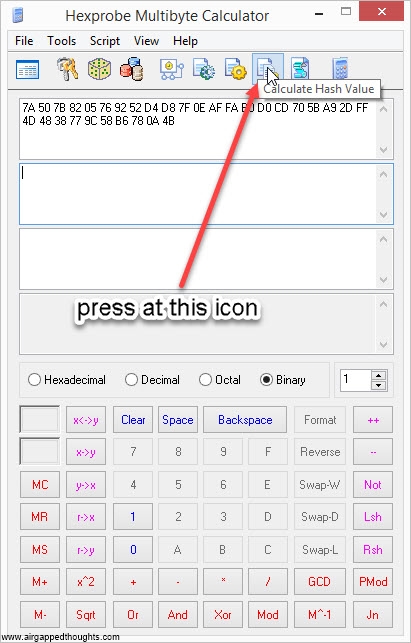
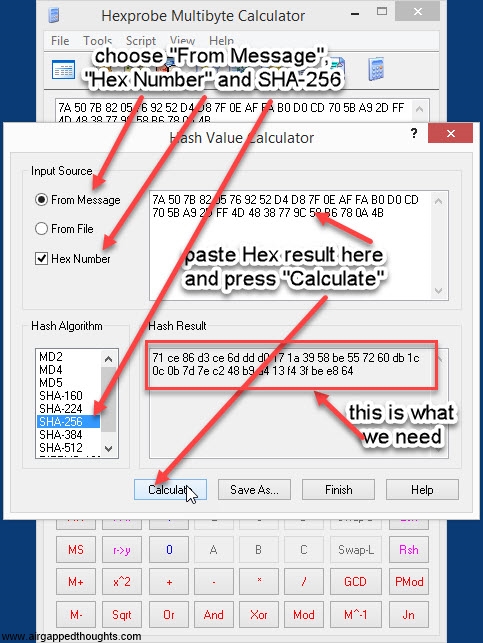
or just go here (only for testing purposes, never use online tools) and paste it to the binary hash field, press the Hash button, and go to the bottom of the page and find the SHA-256 result which (for our entropy) is going to be:
71ce86d3ce6dddd0171a3958be557260db1c0c0b7d7ec248b9a413f43fbee864
3. The above conversions were necessary so we can get our checksum. The checksum is responsible for the validity of our mnemonic seed and works as the last mnemonic seed word (the 12th, 18th or 24th word in our mnemonic), this is very important and you should be very careful not to make any mistake (although you’ll probably wont find any wallet that accepts mnemonics with wrong checksum). Depending in the length of our entropy (which is 256bit long in our example), we need a different length of checksum. To find the required length, we divide the entrophy.length / 32 which in our example is 256 / 32 = 8. We need 8 bits of entropy. We always take them from the very start of the hashed value, which in our example is the number 71:
71ce86d3ce6dddd0171a3958be557260db1c0c0b7d7ec248b9a413f43fbee864
Now you might wonder why we took 2 digits and not 8? That’s because this is a hexadecimal value. Each hexadecimal character represents 4 bits, and so 71 actually represents 8 bits.
We once again have to use Hexprobe Multibyte Calculator and do a hexadecimal to binary conversion:
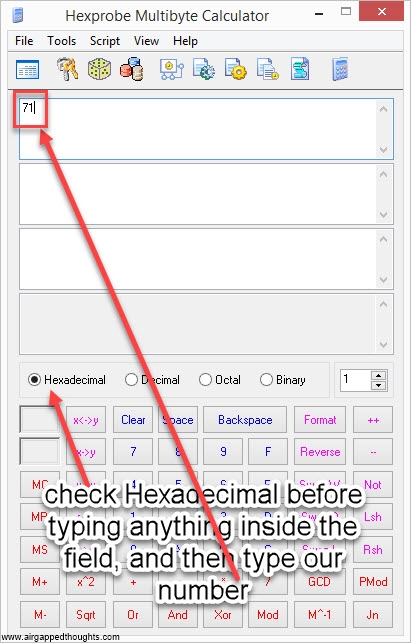
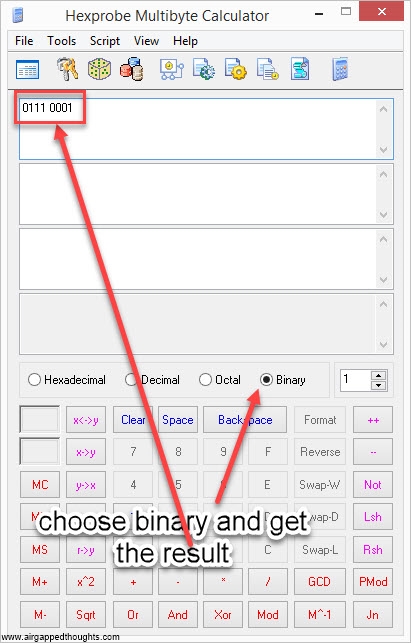
or use this online tool, the result in our example is:
01110001 [this is our checksum]
4. Now let’s go to our entropy and put our checksum at the end of it:
011110100101000001111011100000100000010101110110100100100101001011010100110110000111111100001110101011111111101010110000110100001100110101110000010110111010100100101101111111110100110101001000001110000111011110011100010110001011011001111000000010100100101101110001
This is our mnemonic! Let’s make it a bit more readable.
5. As a said earlier, every 11 bits is one word. By making small chunks of 11 bits each, our entropy (which is now 256 + 8 = 264 bit long) will be split into 24 parts (got it?)
01111010010 10000011110 11100000100 00001010111 01101001001 00101001011 01010011011 00001111111 00001110101 01111111110 10101100001 10100001100 11010111000 00101101110 10100100101 10111111111 01001101010 01000001110 00011101111 00111000101 10001011011 00111100000 00101001001 01101110001
6. Now we have to transform these binary values into words. To do that, we have to make a conversion for each one of these chunks, from binary to decimal. Once again, we’re going to use Hexprobe Multibyte Calculator, the picture is for the first part of the entropy (01111010010), you’ll have to repeat it for every part:
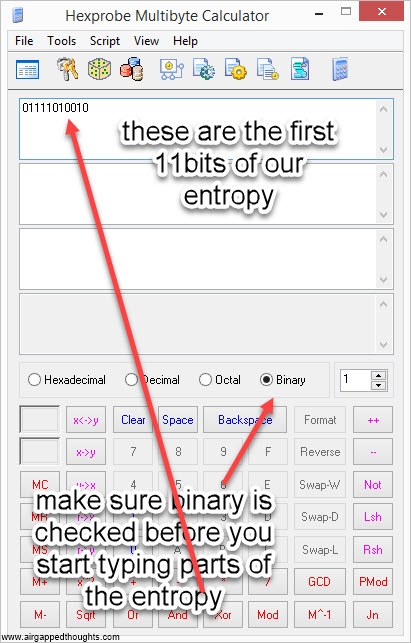
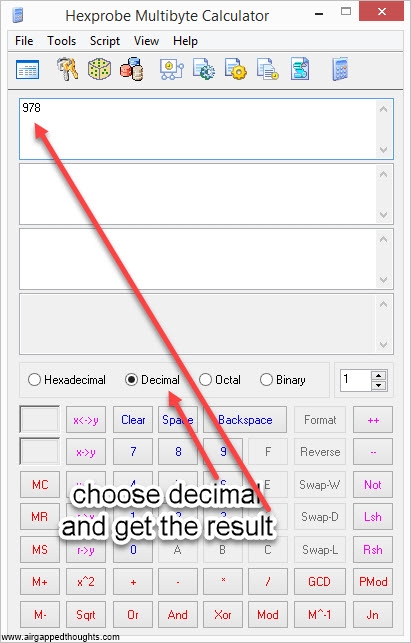
or use this online tool, keep in mind that’s totally unsafe since you’re going to give your whole entropy / mnemonic seed to some server, use it only for testing purposes. This will give us a number from 0 to 2047. The above chunks will turn to:
01111010010 = 978
10000011110 = 1054
11100000100 = 1796
00001010111 = 87
01101001001 = 841
00101001011 = 331
01010011011 = 667
00001111111 = 127
00001110101 = 117
01111111110 = 1022
10101100001 = 1377
10100001100 = 1292
11010111000 = 1720
00101101110 = 366
10100100101 = 1317
10111111111 = 1535
01001101010 = 618
01000001110 = 526
00011101111 = 239
00111000101 = 453
10001011011 = 1115
00111100000 = 480
00101001001 = 329
01101110001 = 881
7. For the final part, we will have to associate the decimal numbers with a word from the official bip39 dictionary which can be found here. Keep in mind that every chunk of the above can give us a number from 0 to 2047. That’s because the lowest possible binary value is 00000000000 which equals to 0 and the highest is 11111111111 which equals to 2047. Meanwhile the bip39 dictionary is numbered from 1 to 2048, so we will have to increase our numbers by 1 to change our limit from 0-2047 to 1-2048. For example, the first decimal number is 978 so we have to change it to 978+1 = 979 which corresponds to the word kid in the dictionary, this is the first word of our mnemonic seed.
1. 01111010010 = 978 + 1 = 979 = kid
2. 10000011110 = 1054 + 1 = 1055 = long
3. 11100000100 = 1796 + 1 = 1797 = they
4. 00001010111 = 87 + 1 = 88 = april
5. 01101001001 = 841 + 1 = 842 = hard
6. 00101001011 = 331 + 1 = 332 = city
7. 01010011011 = 667 + 1 = 668 = fat
8. 00001111111 = 127 + 1 = 128 = avocado
9. 00001110101 = 117 + 1 = 118 = attitude
10. 01111111110 = 1022 + 1 = 1023 = lemon
11. 10101100001 = 1377 + 1 = 1378 = promote
12. 10100001100 = 1292 + 1 = 1293 = pave
13. 11010111000 = 1720 + 1721 = strike
14. 00101101110 = 366 + 1 = 367= column
15. 10100100101 = 1317 + 1 = 1318 = pigeon
16. 10111111111 = 1535 + 1 = 1536 = say
17. 01001101010 = 618 + 1 = 619 = essence
18. 01000001110 = 526 + 1 = 527 = dove
19. 00011101111 = 239 + 1 = 240 = bulb
20. 00111000101 = 453 + 1 = 454 = december
21. 10001011011 = 1115 + 1 = 1116 = merge
22. 00111100000 = 480 + 1 = 481 = despair
23. 00101001001 = 329 + 1 = 330 = circle
24. 01101110001 = 881 + 1 = 882 = hotel
There you go! Our mnemonic seed, completely handmade:
kid long they april hard city fat avocado attitude lemon promote pave
strike column pigeon say essence dove bulb december merge despair circle hotel
DO NOT USE THE ABOVE MNEMONIC SEED UNLESS YOU LOVE LIVING IN DANGER
If you’d like to make a 12 or 18 words mnemonic seed don’t forget that both entropy length and checksum length must be different from the above example. Every other step remains exactly the same. A 18 words mnemonic (192 bits of entropy) will have a 192/32=6 bits of entropy. This means that you will have to take 2 digits from the hashed value, turn them into decimal, and from the 8 resulted bits, you will only need to take the 6 first as a checksum and ignore the other 2.
Let’s do a quick example:
192 random bits of entropy (18 words mnemonic seed)
111011001011001110010101101001101000001001010111110000001010001110001000110100000011000010010000000111011010001100001100001100110010110010101000111101000011000010111100001000010001010111000000
Entropy to hexadecimal
ECB395A68257C0A388D030901DA30C332CA8F430BC2115C0
Hashed
8a67ad8582ed607d0745d0ec7184bfa05437f53d5ab3090cda832388118ecf55
Entropy —-> 192/32 = 6 bits so:
8a67ad8582ed607d0745d0ec7184bfa05437f53d5ab3090cda832388118ecf55
Turn 8a into decimal: 10001010
we only need 6 bits so we only take the first 6 digits as checksum: 10001010
Put the checksum at the end of our entropy
111011001011001110010101101001101000001001010111110000001010001110001000110100000011000010010000000111011010001100001100001100110010110010101000111101000011000010111100001000010001010111000000100010
Split entropy into chunks of 11bits
11101100101 10011100101 01101001101 00000100101 01111100000 01010001110 00100011010 00000110000 10010000000 11101101000 11000011000 01100110010 11001010100 01111010000 11000010111 10000100001 00010101110 00000100010
Notice that if our checksum wasnt 6 bits, the last chunk wouldnt be 11 bits (5 + 6 of the checksum) which is a requirement. Thats why we take different checksum length for different entropy length. The last chunk in the 256bit entropy example, was actually just 3 bits long and so we needed 8 bits of checksum (don’t forget to use entropy.length / 32 to find the required checksum length although you can also figure it out from the last chunk of the divided entropy).
Let’s turn these chunks into decimal
11101100101 (1893) 10011100101 (1253) 01101001101 (845) 00000100101 (37) 01111100000 (992) 01010001110 (654) 00100011010 (282) 00000110000 (48) 10010000000 (1152) 11101101000 (1896) 11000011000 (1560) 01100110010 (818) 11001010100 (1620) 01111010000 (976) 11000010111 (1559) 10000100001 (1057) 00010101110 (174) 00000100010 (34)
And now let’s turn them into words from the bip39 dictionary. Don’t forget to add +1 to each decimal number to obtain the right words otherwise you’ll end up with a totally invalid mnemonic with invalid checksum.
1894=uncover 1254=original 846=have 38=again 993=lab 655=fade
283=cash 49=alcohol 1153=mosquito 1897=unfair 1561=seek 819=green
1621=skin 977=key 1560=seed 1058=loud 175=beyond 35=affair
Here it is! Our 18 words mnemonic seed:
uncover original have again lab fade
cash alcohol mosquito unfair seek green
skin key seed loud beyond affair
DO NOT USE THE ABOVE MNEMONIC SEED FOR STORING ASSETS!!!


